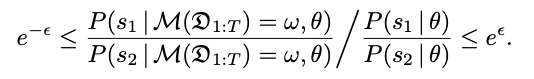What Can Differential Privacy Actually Protect?

Posted on by Kee Siong Ng

Differential Privacy (DP) is, by now, the most widely adopted formal model of privacy protection used in industry [L23] and government [ABS22] but my sense is that its “semantics”, especially in the presence of correlated data and in the adversarial interactive setting, is still not broadly understood in the community, especially among practitioners. In the current post, I will try to describe succinctly what DP can protect, and what it can’t. (See this earlier post if you want to know how DP came from database reconstruction attacks.)

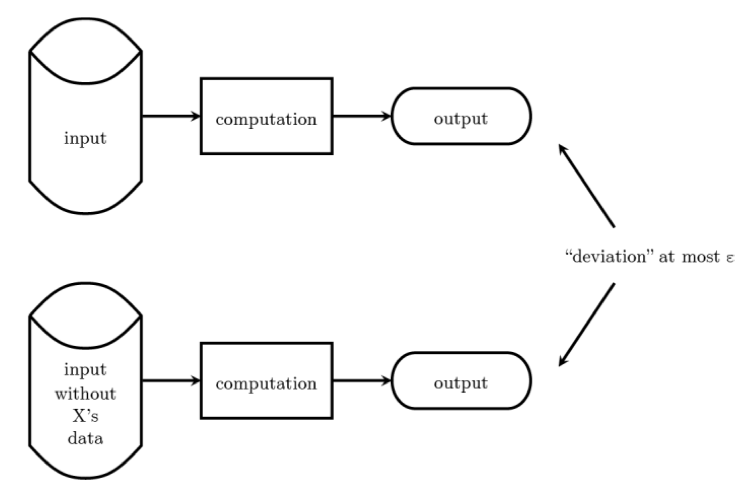
The following diagram from [N16] illustrates the gist of what it means for a computation on data to be differentially private.

Figure 1: Differential Privacy illustrated

The top row shows the output R obtained by performing a computation C on an input dataset D. The bottom row shows the output R’ obtained by performing the same computation C on another dataset D’ obtained from D by removing an arbitrary person X’s data. We say C, which needs to be a computation with some in-built randomisation, is differentially private if the probabilities of seeing R and R’ are very close and can be controlled by a user-demanded parameter epsilon, with lower values of epsilon signalling a higher degree of privacy requirements. (One can think of epsilon as controlling the amount of randomised noise, commensurate with the maximum change to the computation output that can result from any one individual’s data, that needs to be introduced, so in practice there is a privacy-utility tradeoff in that the value of the output will lose utility as more and more noise are injected. In fact, if one doesn’t care about utility, then one can always get privacy.)

Looking at Figure 1, we can conclude that what can be learned about X from a differentially private computation is essentially limited to what can be learned about X from everyone else’s data without X being included in the computation. And, obviously, this guarantee applies to everyone in the input dataset D, since the choice of X is arbitrary.

Note carefully here that the privacy protection offered to X is basically plausible deniability on the “presence” of X’s data in the input dataset, but not the actual value of X’s data. It turns out that it is essentially impossible to protect the value of X’s data when there are correlations in the data, at least if we want to preserve the output’s utility. Here are a few examples to illustrate the issue.

Example 1 (adapted from [KS14]): Consider an insurance assessor, Alice, who possesses prior knowledge that a customer, John, regularly smokes. If a clinical study reports a meaningful causal relationship between smoking and lung disease, it would lead Alice to conclude that John has a higher risk of lung disease compared to non-smokers and therefore should have his insurance premium increased. This occurs regardless of whether John actually participated in the clinical study. What DP provides in this case is only that John’s insurance premium increase is *not* due to the presence of his data in the clinical study.

Example 2 (adapted from [YN24]): Consider a highly contagious and long recovery flu spreading in a tight-knit community of individuals living in close quarters. This can be modelled as an SEIRS epidemic model on a fully connected contact network. Given the flu’s characteristics and the fully connected contact network, we can say with high probability either all individuals or no individuals are infected at any one time. Suppose we sample some individuals from time to time and report on their infection status. Even with differentially private noise, an adversary will, with high probability, guess the flu status of any one individual in the community, regardless of whether they are in the sample. Again, correlation is the issue here.

So what can differential privacy actually protect? Or put another way, if DP is the solution (given its popularity), what is the problem it solves?

There are multiple ways to define and understand the semantics of differential privacy, and these studies clarify what protection DP actually provides. One is based on a Bayesian interpretation, which started with [KS14] and has evolved into a general mathematical framework called Pufferfish Privacy [KM14] for defining secrets and adversaries (in the form of possible data-generating processes). In particular, given any secret pair (s1, s2) that we want to protect, an adaptive data-generating process theta representing a possible adversary, we say a (probabilistic) computation M satisfies Pufferfish Privacy for a desired user-supplied privacy parameter if

Here, the probability is over the randomness in the data-generating process theta that produces the possible input dataset \mathfrak{D}_{1:T} over T time steps, and the randomness in the computation M. Note also that for small epsilon, the lower and upper bounds can be interpreted as 1 – epsilon and 1 + epsilon. In other words, Pufferfish Privacy guarantees that, for any possible adversary, the odds ratio of his prior belief in the secrets s1 and s2 is not much different from the odds ratio of his posterior belief in s1 and s2 after seeing the output of the computation. So whatever secret pairs we want to protect, Pufferfish guarantees that an adversary does not get any information to non-trivially improve their ability to distinguish between s1 and s2 after seeing the computation output. Note however that we are not saying s1 and s2 are indistinguishable to the adversary to begin with — for example, it may well be known to the adversary from prior knowledge that s1 is much more likely than s2 and this is fine — only that an adversary’s ability to distinguish between s1 and s2 does not improve from what he already knows from prior knowledge after seeing the computation output.

[KM14] shows in their Theorem 6.1 that Differential Privacy satisfies Pufferfish Privacy in the case where the secret pairs (s1, s2) take the form of s1 and s2 being input datasets that differ in exactly one row (refer to Figure 1 above), and the data-generating process theta satisfies the constraint that all the records in s1 (and s2) are generated independently of each other, which means there are no correlation in the input dataset. This result was subsequently generalised to the adaptive / interactive case for population processes in Lemma 1 in [YN24], where there can be correlation in the data in the underlying stochastic population process — an example is an epidemic or misinformation spreading in a population represented by a contact network — but individuals are sampled independently of each other at every time step. The secret pairs that can be protected are exactly on whether an (arbitrary) individual’s data is present in the dataset collected at any of the time steps, but not on the actual value of the individual’s data, which one can show cannot be protected in general.

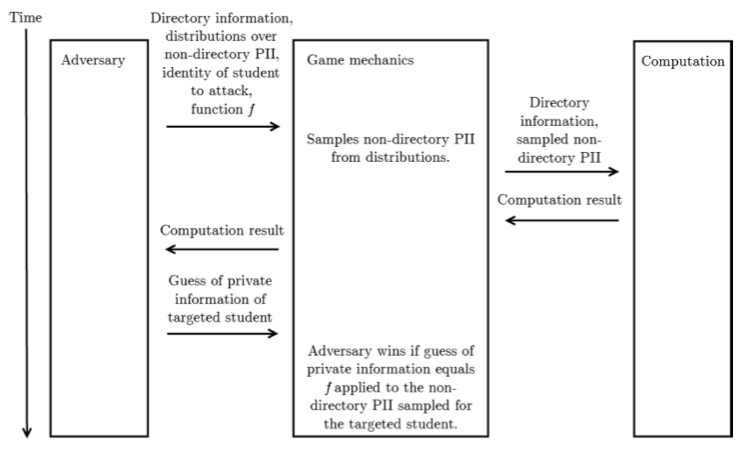
A second, related, way to give semantics to DP is via Privacy Games. This is the approach taken in [N16], where the authors analysed the text and case law of privacy requirements in relevant US legislation (e.g. FERPA or the HIPAA Privacy rule) like “the risk is very small that the information could be used, alone or in combination with other reasonably available information, by an anticipated recipient to identify an individual who is a subject of the information” and construct privacy games like the one shown in the following diagram (Figure 7 in [N16]), which contains a model of what an adversary knows from prior knowledge, a computation that we want to show is private, and a game mechanics that describes how the adversary interacts with the computation.

In the specific privacy game above, which is designed to capture privacy requirements in the Family Education Rights and Privacy Act (FERPA), the adversary has access to some publicly available information known as “directory information” and prior belief on the personally identifiable information of individuals (in terms of a probability distribution on the unknown attributes), and it seeks to determine whether it can find out the private information of a specific targeted individual. The adversary wins if his probability of guessing the private information of the targeted individual is non-trivially higher after seeing the result of the computation compared to the probability from his prior belief. (You can see the similarity to the Pufferfish privacy requirement here. In a way, privacy games are “imperative” versions of the “declarative” Pufferfish privacy requirement.)

Under the assumption that the records in a dataset are generated independently (so, again, no correlation), [N16] shows, using the hybrid games proof technique that originated in [GM84], that differentially private computations do not give adversaries any non-trivial edge in winning a collection of conservatively designed privacy games extracted from FERPA. That is reassuring, but the assumption that the data has no correlation is problematic.

And note that we have reached the same place via two different paths, given that the Pufferfish analysis of Differential Privacy also needed the assumption that the dataset contains no correlation between records. Now, while it is relatively easy to ensure no correlation in the presence or absence of a specific individual’s data in a dataset — just sample each individual independently (but not necessarily with the same probability distribution) — I have personally never seen a real dataset where the values of the records in the dataset are not correlated in some way. Structures exist in most natural phenomenon we care about and those structures shows up as correlations in the values of the data we collect!

So where does the above analysis leave us in a world with (i) increasingly available, either publicly or commercially, datasets on just about anything anyone cares about, and (ii) increasingly sophisticated Machine Learning / AI algorithms for finding correlations in those datasets?

I don’t have the full answer, obviously, but here are some thoughts.

The first is not to blindly take a widely adopted notion like Differential Privacy as the panacea to our privacy concerns without reading the fine prints. Try to understand the math in detail if one is equipped to do so, or at least read articles like this one if math is not your thing. If the privacy issue in a specific context can be addressed through plausible deniability on the presence or otherwise of one’s data in a dataset of interest, then DP is likely a good answer. But there are many privacy scenarios where that is not good enough.

And that brings me to my second point, which is that we should, as much as possible, take a bottom up approach when it comes to analysing privacy issues. I consider [N16] as best practice, where the authors first analyse the privacy requirements from the actual text and case law of privacy legislation and regulations, then construct suitable and conservative mathematical models of the type of adversaries and privacy protections intended by law, and finally attempt to show how privacy mechanisms either address or don’t address those privacy requirements. The techniques described in [A20] are also incredibly useful for analysing whether and how the typical steps of a computation we want to perform on data can leak information to an adversary. There is no substitute for context and hard work.

The last point I want to make is that there are actually general privacy mechanisms like the Wasserstein Mechanism [SWC17] that would allow one to quantify the amount of correlation in a dataset and then introduce appropriate noise to provide the Pufferfish Privacy guarantee. The catch is that the Wasserstein Mechanism is hard to compute exactly in general, although there are special cases where the Wasserstein metric can be calculated exactly or at least approximated well (say using the Sinkhorn algorithm). And that’s another argument for taking the bottom up approach to analyse your specific privacy requirements, and hope that you’re in one of those special cases where even though Differential Privacy isn’t quite enough, a specific instantiation of the Wasserstein Mechanism can be computed fast enough to achieve what you need.

References

Leave a comment