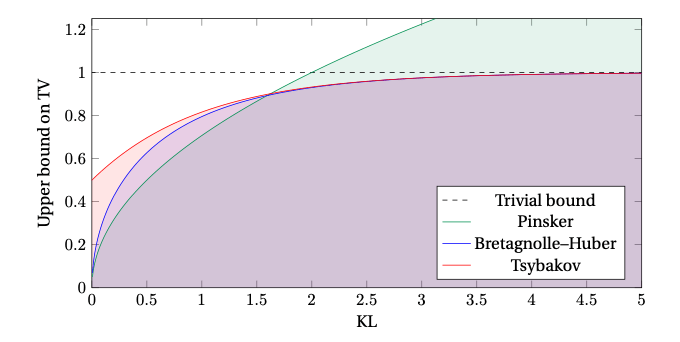
The Bretagnolle-Huber Inequality provides a bound on the total variation distance between two probability distributions in terms of their Kullback-Leibler divergence, and it is better than Pinsker’s Inequality when the KL divergence is larger than two, and it is never vacuous, as shown in this figure from [Canonne2023].
The following is an elementary proof, which is essentially what is in [Canonne2023] and apparently the original proof in [Bretagnolle1979], but hopefully the presentation is less magical. We first give the definition of total variation distance and a key property.

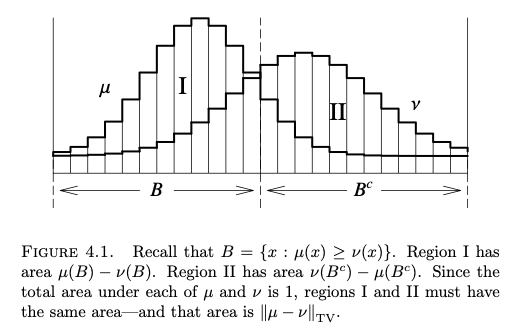
The proof can be found in many standard textbooks. This diagram from [Levin2017] gives the key insights on Equation (1).
Given the above, we can now give the proof. The proof is simpler than what is on Wikipedia, which involves both the Cauchy-Schwarz inequality and Jensen’s inequality. We only need the latter below.

Enjoy.
[Cannone2023] Clement L. Cannone, A short note on an inequality between KL and TV, https://arxiv.org/pdf/2202.07198
[Bretagnolle1979] Jean Bretagnolle and Catherine Huber, Estimation des densités: risque minimax.
[Levin2017] David Levin and Yuval Peres, Markov Chains and Mixing Times, 2017 https://pages.uoregon.edu/dlevin/MARKOV/markovmixing.pdf